Statistische Berechnungen
In der Statistik werden verschiedene Parameter zur Beschreibung von Eigenschaften einer Häufigkeitsverteilung verwendet.
Der beim Beispiel auf der Seite Statistik berechnete Median ist ein Quantil.
- Quantile sind ein Streuungsmaß in der Statistik.
- Quantile sind Kennzahlen für Messreihen und Verteilungen
- Quantile sind Punkte einer nach Rang oder Größe der Einzelwerte sortierten statistischen Verteilung.
Besondere Quantile sind:
- Median (auch Zentralwert, Einteilung der gesamten Verteilung in zwei gleich große Teile)
- Quartil (auch Viertelwerte, Einteilung der zugrunde liegenden Verteilung in vier Viertel.)
- Quintil (auch Fünftelwerte, Einteilung der zugrunde liegenden Verteilung in fünf Fünftel.)
- Dezil (auch Zehntelwerte, die Verteilung wird in 10 gleich große Teile zerlegt)
- Perzentil (auch Hundertstelwerte, die Verteilung wird in 100 gleich große Teile zerlegt)
Wenn man also eine reale Einschätzung der Einkommens- und Vermögenssituation eines Staates machen will, muss man Quantile verwenden. Ein Durchschnittswert einer Gesamtheit kann steigen und auch sehr hoch sein, der größte Teil der Gesamtheit liegt aber weit unter dem Durchschnittswert. Verwendet man aber zur Untersuchung z. B. Dezile ergeben sich plötzlich ganz andere Aussagen.
Wenn man die Bevölkerung in 10 gleich große Gruppen (Dezile) einteilt und ermittelt wie viel Prozent jede Gruppe am Gesamteinkommen verdient, wird man erstaunliches feststellen. Erschreckend wird es, wenn man diese Zahlen noch über einen gewissen Zeitablauf betrachtet.
Um die weiteren Berechnungen zu verstehen, folgt hier noch etwas Theorie zur Lorenzkurve.
Die Lorenzkurve ist eine grafische Darstellung zur Veranschaulichung der Einkommensverteilung in einer Volkswirtschaft. Sie wurde erstmals 1905 von dem amerikanischen Statistiker Max O. Lorenz veröffentlicht. Die Lorenzkurve zeigt, wie viel Prozent der Einkommensempfänger in einer Volkswirtschaft wie viel Prozent des Volkseinkommens verdienen. Verdient jeder gleich viel, ergibt sich eine Gerade (Diagonale). Die Diagonale würde eine theoretische Gleichverteilung der Einkommen bedeuten. Die Entfernung der Kurve der tatsächlichen Einkommensverteilung von der Diagonale bedeutet also eine ungleiche Einkommensverteilung und damit Einkommensunterschiede.
Bei der Lorenzkurve wird eine bestimmte Größe (z. B. das Einkommen) beim kleinsten Wert beginnend sortiert und anschließend aufaddiert (kumuliert). Am folgenden Beispiel lässt sich das gut demonstrieren:
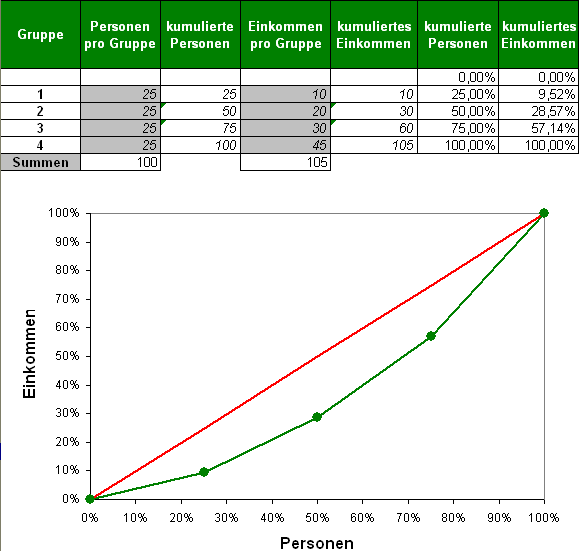
Wir haben hier 4 Gruppen von Einkommensempfängern mit einem unterschiedlichen Einkommen. Die Gruppen wurden nach der Einkommenshöhe sortiert, die Personenzahl und das Einkommen aufaddiert (kumuliert) und die absoluten Werte in Prozentangaben umgerechnet. Jetzt ergeben sich folgende Aussagen:
- 25% der Personen bekommen 9,52% des Einkommens
- 50% der Personen bekommen 28,57% des Einkommens
- 75% der Personen bekommen 57,14% des Einkommens
- die Gruppe mit dem höchsten Einkommen (auch 25%) erhält 42,86% des Einkommens
Die rote Linie wäre eine totale Gleichverteilung. Dabei wäre die Lorenz-Kurve eine gerade Linie von Punkt 0/0 zu Punkt 1/1.
Mit der Lorenzkurve lassen sich also Merkmale bezüglich ihrer Konzentrationsverteilung darstellen. Sie kann auch zur Darstellung der Marktmacht verwendet werden.
Auch die ABC-Analyse ist eine Anwendung der Lorenzkurve. Die ABC-Analyse ist ein betriebswirtschaftliches Analyseverfahren zur Gewichtung von Objekten oder Prozessen und wird beispielsweise dazu verwendet, den Materialverbrauch nach Wertgrößen zu gruppieren.
In dem obigen Beispiel sehen wir also eine Ungleichverteilung des Einkommens. In der Statistik gibt es Ungleichverteilungsmaße zur Beschreibung des Grades der Ungleichverteilung einer Größe gegenüber einer anderen Größe. Einer davon ist der Gini-Koeffizient.
Der Gini-Koeffizient ist eine statistische Maßgröße, die vom italienischen Statistiker Corrado Gini zur Darstellung von Ungleichverteilungen entwickelt wurde. Die Berechnungen beruhen auf dem Konzept der Lorenzkurve. Bei völliger Gleichverteilung ist der Gini-Koeffizient gleich 0 und bei vollkommener Konzentration gleich 1. Je näher der Gini-Koeffizient also am Wert 1 ist, desto größer ist die Ungleichverteilung.
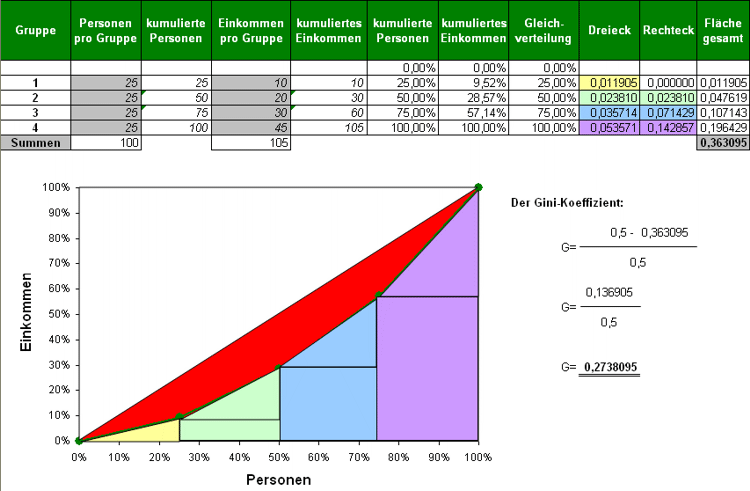
Zur Ermittlung wird die Fläche zwischen der Kurve der totalen Gleichverteilung und der Fläche unterhalb der Kurve der tatsächlichen Verteilung durch die Fläche unterhalb der Kurve der totalen Gleichverteilung dividiert (siehe Grafik).
Schritte zur Berechnung:
- Berechnung der Fläche unter der Kurve der totalen Gleichverteilung (1 * 1 /2 = 0,5).
- Berechnung der Fläche unter der Kurve der tatsächlichen Verteilung (Dreiecke und Rechtecke der Grafik).
- Berechnung der Fläche zwischen der Kurve der totalen Gleichverteilung und der Kurve der tatsächlichen Verteilung (rote Fläche der Grafik):
Fläche aus Schritt 1 minus Fläche aus Schritt 2 - Fläche aus Schritt 3 dividiert durch Fläche aus Schritt 1 ergibt den Gini-Koeffizient
Der Wochenbericht 8/2015 des DIW (Deutsches Institut für Wirtschaftsforschung e.V.) enthält zum Einfluss der Sozialversicherung auf den Gini-Koeffizient einen Beitrag.
Auszug aus dem Inhalt:
Die monetäre Umverteilung durch das Steuer- und Transfersystem führt insgesamt dazu, dass die Nettoeinkommen in Deutschland deutlich gleichmäßiger verteilt sind als die Markteinkommen. So sinkt der Gini-Koeffizient von 0,5 für die Markteinkommen auf 0,29 für die verfügbaren Haushaltseinkommen im Jahr 2011. Einen maßgeblichen Anteil an der gesamten staatlichen Umverteilung hat das Sozialversicherungssystem, das mehr als die Hälfte der Ungleichheitsreduktion ausmacht. Soweit für die Sozialversicherungsleistungen versicherungsäquivalente Beiträge erhoben werden, findet aber im Zeitverlauf letztlich keine Umverteilung zwischen Personen oder Generationen statt.
Der DIW Wochenbericht 10/2017 des DIW (Deutsches Institut für Wirtschaftsforschung e.V.) enthält den Bericht "Wie steigende Einkommensungleichheit das Wirtschaftswachstum in Deutschland beeinflusst".
Auszug aus dem Inhalt:
Vor allem die private Konsumnachfrage, aber auch Investitionen und Exporte, wären stärker gestiegen, wenn die Ungleichheit - hier gemessen am Gini-Koeffizienten der Nettohaushaltseinkommen - auf ihrem Stand des Jahres 1991 geblieben wäre. Gleichzeitig hätte der Außenhandelssaldo nicht so stark zugenommen; er hat den Effekt der Ungleichheit auf das Bruttoinlandsprodukt abgemildert.
Auszug aus der Pressemitteilung vom 15. Dezember 2021 des DIW (Deutsches Institut für Wirtschaftsforschung e.V.):
DIW-Berechnungen zeigen, wie ein Grunderbe die Vermögensungleichheit verringern würde - Finanzierung durch vermögensbezogene Steuern sinnvoll - Beide Komponenten zusammen würden Vermögensungleichheit gemessen am Gini-Koeffizienten um bis zu sieben Prozent senken
Ein Grunderbe in Höhe von bis zu 20.000 Euro für alle 18-Jährigen und deren Finanzierung durch Erbschaftsteuer oder Vermögensteuer würde die Vermögensungleichheit in Deutschland deutlich reduzieren. Je nach Ausgestaltung sänke der Gini-Koeffizient, das Standardmaß der Ungleichheit, um fünf bis sieben Prozent. Das ist das zentrale Ergebnis einer Simulationsberechnung des Deutschen Instituts für Wirtschaftsforschung (DIW Berlin).
© 2007-2024 A.Liebig - Impressum - Kontakt - Datenschutz - Inhaltsverzeichnis (Sitemap) - Lohnlexikon